So maybe you are coming from desktop or server programming, or you have already played with platforms like Arduino, and now you would like to enter the real-time embedded system world, especially using RTOS. Then you need to know some basic concepts. This is what this series of post will be about.
In real-time systems, unit of code are grouped in tasks. There are several kinds of tasks that can be classified based on certain characteristics such as their activation patterns:
- Periodic
- A periodic task is one who is activated repeteadly with a fixed duration between two successive executions (aka instances of the task), i.e. whose code will executed every X ms.
- Aperiodic
- An aperiodic task will be executed at some unknown points in time, for example by an external trigger such an I/O changing value.
- Sporadic
- A sporadic task is basically an aperiodic task but we can still provide a minimal interarrival time, i.e. the smallest duration between the end of an execution and the following activation. The benefit of sporadic tasks over aperiodic tasks is that the workload submitted to the system is bounded, which is prerequisite to ensure a predictable timing behaviour.
Of course, there are many variations around those 3 basic task models, such as the more expressive generalized multi-frame task model where both the minimal interarrival time and the execution time can change (in a predefined manner though) from one instance of the task to another.
In CPAL, you would implement those 3 types of tasks like this:
processdef Some_Code()
{
state Main {
}
}
process Some_Code: periodic_task_1[200ms]();
process Some_Code: aperiodic_task_2[][bool.as(uint8.rand_uniform(0,1))]();
const time64: T3_MIT = 100ms; /* The minimum interarrival time of sporadic_task_3. */
process Some_Code: sporadic_task_3[T3_MIT]();
@cpal:time:sporadic_task_3
{
/*At each activation, we will compute the time to the next activation. */
sporadic_task_3.period = time64.rand_uniform(T3_MIT, 300ms);
}
As can be seen in the code above, periodic and sporadic tasks are straightforward to implement in CPAL, but sporadic tasks require a timing annotation where the next activation time is scheduled. We should note that this annotation is for modeling and simulation purpose only, on the real system the sporadic task could be implemented as an aperiodic tasks that happens when it happens but for which we know for sure (and this can be verified and controlled at run-time) that it will not be executed more often than its minimal inter-arrival time.
In most cases a real-time system will contain many tasks, several hundreds sometimes such as in automotive dashboards, and several may be ready to execute at the same time. One thus needs to describe how to arbitrate between them by deciding their order of execution. This is what the scheduling policy does.
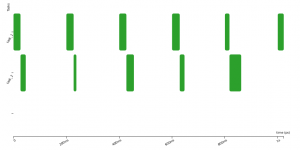
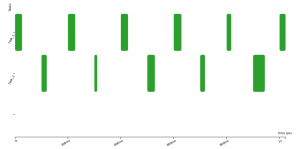
In the following example, two tasks are released at times t=0s, t=100ms, t=200ms, … It is obviously not possible that they execute at the same time on a single cpu platform.
process Some_Code: task_1[200ms]();
process Some_Code: task_2[200ms]();
The scheduling policy needs to base its decision on some criteria. It can be simply a priority that is given to each task. It means that every time several tasks are pending execution, the one with highest priority will be executed first – this is called Fixed-Priority scheduling. Another simple policy is FIFO, First-In First-Out, where the execution order is decided based on the arrival times (i.e., release times) of the instances of the tasks. An other common policy is based on an attribute called the deadline. Indeed, in real-time systems usually, for a task to be useful for the system, it shall be finished before a given time point called the deadline. In most cases, the deadline is less than or equal to the period of the task.
@cpal:time
{
task_1.deadline = 100ms;
task_2.deadline = 90ms;
assert(task_1.deadline <= task_1.period);
assert(task_2.deadline <= task_2.period);
}
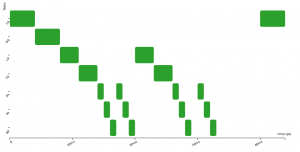
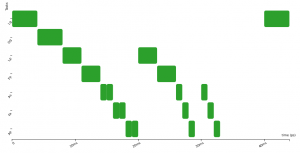
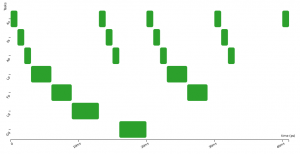
Here are three activation diagrams (of a more complex example), the first using FIFO scheduling, the second with Non-Preemptive Fixed-Priority scheduler (NPFP), and third with Non-Preemptive Earliest-Deadline-First (NPEDF). These three policies are available in CPAL.
As you can see, the successive executions of a task are not strictly periodic (e.g., second and third row). There are some variations, “jitters”, between the start of execution of successive instances. In control systems, these “start-of-execution” jitters are usually detrimental to the quality of the control, possibly leading to faulty behaviours. To overcome this, we can try to optimise the system by using an offset, that is by shifting in time the executions of some tasks so that they are no more, or less often, in conflict for the access to the CPU. Below the offset of task_2 is set to 100ms and this avoids any conflicts with task_1.
process Some_Code: task_1[200ms]();
process Some_Code: task_2[200ms, 100ms]();
A system (i.e., a set of tasks + a scheduling policy) is said to be feasible provided that all activations of all tasks respect their deadline (there might be other requirements than deadlines in some systems, low jitters or execution precedence contraints for instance). With CPAL, we can use simulation to check feasibility by monitoring at run-time if the deadlines are met.
processdef Deadline_Checker()
{
static var uint64: i =0;
state Main {
IO.println("%u Current End of execution:\t%t", self.pid, self.current_activation + self.execution_time);
IO.println("%u Current Activation Deadline:\t%t", self.pid, self.offset + i * self.period + self.deadline);
assert(self.execution_time + self.current_activation <= self.offset + self.deadline + i * self.period);
i=i+1;
}
}
process Deadline_Checker: task_1[200ms]();
process Deadline_Checker: task_2[200ms]();
@cpal:time
{
task_1.deadline = 100ms;
task_2.deadline = 90ms;
assert(task_1.deadline <= task_1.period);
assert(task_2.deadline <= task_2.period);
}
@cpal:time:task_1
{
task_1.execution_time = time64.rand_uniform(10ms, 30ms);
}
@cpal:time:task_2
{
task_2.execution_time = time64.rand_uniform(10ms, 60ms);
}
/*
process Deadline_Checker: big_slow_task_3[500ms]();
@cpal:time:big_slow_task_3
{
big_slow_task_3.execution_time = time64.rand_uniform(100ms, 499ms);
}
*/
It is also feasible, and sometimes required for instance when the simulation cannot be exhaustive, to check deadline respect using a “schedulability analysis” like done in this paper for the FIFO scheduling policy with offsets of CPAL.
In real systems sometimes it is hard to come up with a feasible scheduling, especially at high load levels. Indeed you may have some big task, i.e. one taking a long time to execute even if less often activated. You can see for instance what happens in the previous example if you decomment the code at the end. A solution is that smaller, more urgent tasks should be able to suspend, that is preempt other tasks. This is what preemptive scheduling policies do, a whole new set of policies.
In future posts, we will explore in more depth how to analyse effects of policies. Interested in these topics? You can subscribe to our Twitter feed to be kept updated about new posts.